| Головна » Статті » Землевпоряднику |
Визначення середніх величин
| Визначення середньої арифметичної зваженої величини Середня арифметична є найбільш поширеним видом середніх величин. Вона може бути простою і зваженою величиною. Середня арифметична проста застосовується у тому разі, якщо окремі значення ознаки трапляються однакове число разів . Її одержують у результаті ділення суми індивідуальних значень ознак на їх кількість за формулою: 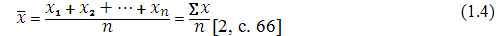 де – середня арифметична величина ознаки; x1, x2, хn – індивідуальні значення ознак; n – кількість індивідуальних значень ознаки. Якщо окремі значення ознаки мають неоднакове число повторень, то визначається середня арифметична зважена величина: 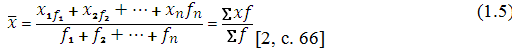 де – питома вага індивідуальних значень ознак. У нашому випадку, аналізуючи показники табл. 3, бачимо, що окремі значення ознаки мають неоднакове число повторень. Тому визначаємо середню арифметичну зважену величину. Зважування в цьому разі проводять за частотами, які показують, скільки разів повторюється певний варіант. Сумарне значення індивідуальних ознак дорівнює 1110 (графа 6). Виходячи із цього, питомою вагою в цьому разі буде загальна кількість контурів(f) (графа 3). Середня арифметична зважена величина для наших значень дорівнює:  Крім середніх арифметичних величин, для характеристики ознак, що визначаються, використовують такі середні величини, як мода і медіана. Визначення середньої величини – моди Модою називають значення ознаки, яке найчастіше повторюється в досліджуваній сукупності. Тобто, це варіант, який має найбільшу частоту. Визначення моди проводимо в такій послідовності: визначення модального інтервалу; визначення значення моди. Модальний інтервал – це інтервал, який має найбільшу частоту. Знайдемо модальний інтервал для нашого прикладу. У графі 3 табл. 3 найбільшу кількість контурів має четверта група з інтервалом від 60 до 80, який і є модальним для цього випадку. Модальне значення ознаки визначають за формулою:  де Хмо – мода; х0 – нижня межа модального інтервалу; h – величина модального інтервалу; fмо – частота модального інтервалу; fмо-1 – частота інтервалу перед модальним; fмо+1 – частота інтервалу після модального. Модальне значення контурів орних земель в нашому випадку складатиме: . 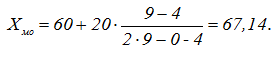 Визначення середньої величини – медіани Медіаною, або середнім варіантом, називають значення ознаки в одиниці сукупності, що займає середнє положення в ранжованому (варіаційному) ряді розподілу. Вона є центром розподілу сукупності і ділить її на дві рівні за кількістю частини. Порядок обчислення медіани такий же самий, як і для моди: визначення медіанного інтервалу та вирахування значення медіани. Спочатку знайдемо медіанний інтервал, тобто інтервал, в якому є значення ознаки, що ділить ряд розподілу на дві рівні частини. При цьому, у великих за чисельністю сукупностях, користуються рядом нагромаджених частот. Так, якщо сукупність складається з парної кількості одиниць, нагромаджені частоти слід поділити на 2 і розрахувати середню з двох центральних варіантів:  де т – медіанний інтервал; f – частота. При непарній кількості одиниць сукупності центр розподілу визначають додаванням до суми частот одиниці і діленням знайдених даних на 2:  де т – медіанний інтервал; f – частота. У нашому випадку згідно з табл. 3 графи 3 сукупність складається з непарної кількості одиниць – 25. Тому для визначення медіанного інтервалу застосовуємо формулу 1.8 і отримуємо:  Отже, тепер у табл. 3 знайдемо, до якого нагромаджуваного ряду (графа 7) належить значення 13. Отримане значення (13) входить до значення 16 нагромаджуваного ряду (графа 7), що відповідає інтервалу 40 – 60, який є медіанним інтервалом для нашого прикладу. Медіанне значення для конкретного інтервального варіаційного ряду визначають за формулою: 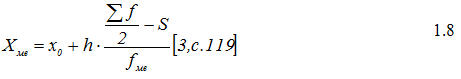 де хме – медіана; х0 – нижня межа медіанного інтервалу; h – величина медіанного інтервалу; f – частоти; S – сума нагромаджених частот перед медіанним інтервалом; f ме – частота медіанного інтервалу. Медіана в інтервальному варіаційному ряду для площ контурів орних земель становить: 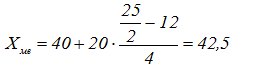 Медіану і моду частіше використовують для характеристики явищ і процесів, про які бракує суцільних даних. У землевпорядкуванні структурні середні величини застосовують при визначенні експертної грошової оцінки, коли з великої кількості значень береться медіанне при застосуванні методу зіставлення цін продажу. За таким же принципом складається групування сільськогосподарських угідь за площею контурів. ТАБЛИЦЯ 3 у попередній статті - "Методи обчислення абсолютних, відносних та середніх величин" Джерело матеріалу: Державний земельний кадастр. Практичний посібник. 2013
| |
| Переглядів: 1860 | | |
| Всього коментарів: 0 | |